前言

为了更方便理解最长递增子序列。所以学习并总结的博客

最长递增子序列

原博客地址

一下是个人总结和觉得重要的知识点

子序列：不一定是连续的
字串：一定是连续的

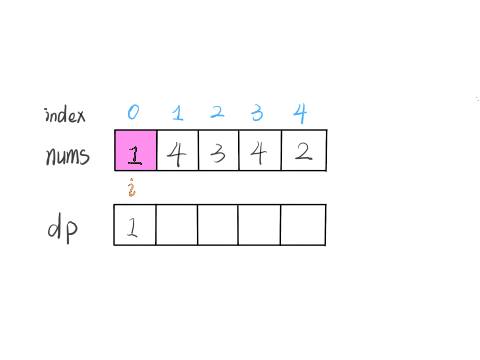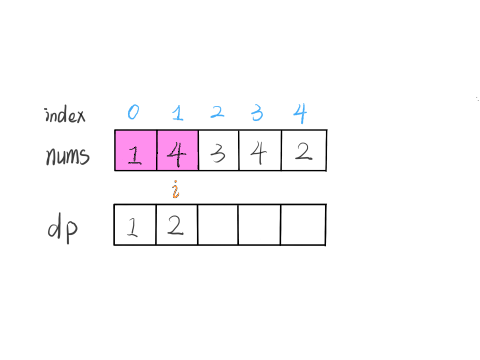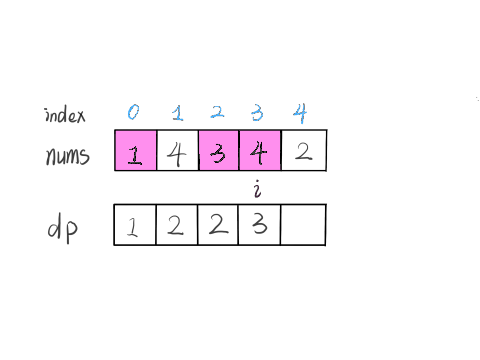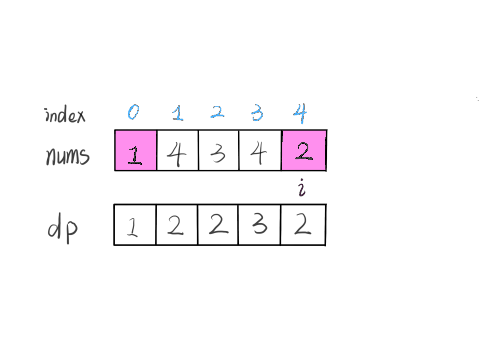
假设一个数组 nums，dp[i] 表示以 nums[i] 这个数结尾的最长递增子序列的长度。

1
2
let nums=[1,4,3,4,2]
//db[3]=3;db[4]=2

这个 GIF 展示了算法演进的过程：
GIF

根据这个定义，我们的最终结果（子序列的最大长度）应该是 dp 数组中的最大值。

1
2
3
4
5
int res = 0;
for (int i = 0; i < dp.length; i++) {
    res = Math.max(res, dp[i]);
}
return res;

那么如何归纳呢 假设我们已经知道了 dp[0..4] 的所有结果，我们如何通过这些已知结果推出 dp[5] 呢?

1
2
3
let nums=[1,4,3,4,2,3]
//db=[1,2,2,3,2] 已知
//db[5]=3?

nums[5] = 3，既然是递增子序列，我们只要找到前面那些结尾比 3 小的子序列，然后把 3 接到这些子序列末尾，就可以形成一个新的递增子序列，而且这个新的子序列长度加一。
nums[5] 前面有哪些元素小于 nums[5]？这个好算，用 for 循环比较一波就能把这些元素找出来。

1
2
3
4
5
6
7
8
// i 为当前我所需要算的db索引
for (int j = 0; j < i; j++) {
    //寻找 nums[0..j-1] 中比 nums[i] 小的元素
    if (nums[i] > nums[j]) {
        // 对比让db[i]一直取到最大的值且加1
        dp[i] = Math.max(dp[i], dp[j] + 1);
    }
}

如上所述，通过归纳法我们已近总结出了算法逻辑了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
function lengthOfLIS(nums:Number[]) {
    // 定义：dp[i] 表示以 nums[i] 这个数结尾的最长递增子序列的长度
     // base case：dp 数组全都初始化为 1
    let dp:Number[] = nums.map(()=>1)
    for (let i = 0; i < nums.length; i++) {
        for (let j = 0; j < i; j++) {
            if (nums[i] > nums[j]) 
                dp[i] = Math.max(dp[i], dp[j] + 1);
        }
    }
    
    let res = 0;
    for (let i = 0; i < dp.length; i++) {
        res = Math.max(res, dp[i]);
    }
    return res;
}